Zero is the integer denoted 0 that, when used as a counting number, means that no objects are present. It is the only integer (and, in fact, the only real number) that is neither negative nor positive. A number which is not zero is said to be nonzero. A root of a function f is also sometimes known as "a zero of f."
Zero is commonly taken to have the factorization ![]() (e.g., in Mathematica's FactorInteger[n] command). On the other hand, the divisors and divisor function
(e.g., in Mathematica's FactorInteger[n] command). On the other hand, the divisors and divisor function ![]() are generally taken to be undefined, since by convention,
are generally taken to be undefined, since by convention, ![]() (i.e., n divides 0) for every n except zero.
(i.e., n divides 0) for every n except zero.
Because the number of permutations of 0 elements is 1, ![]() (zero factorial) is defined as 1 (Wells 1986, p. 31). This definition is useful in expressing many mathematical identities in simple form.
(zero factorial) is defined as 1 (Wells 1986, p. 31). This definition is useful in expressing many mathematical identities in simple form.
A number other than 0 taken to the power 0 is defined to be 1, but 00 itself is undefined. The lack of a well-defined meaning for this quantity follows from the mutually contradictory facts that ![]() is always 1, so 00 should equal 1, but
is always 1, so 00 should equal 1, but ![]() is always 0, so 00 should equal 0. It could be argued that
is always 0, so 00 should equal 0. It could be argued that ![]() is a natural definition since
is a natural definition since
However, the limit does not exist for general complex values of n.
Therefore, the choice of definite for 00 can be made for convenience depending on the problem under consideration. Defining ![]() allows some formulas to be expressed simply (Knuth 1992; Knuth 1997, p. 57), and an example of which is the beautiful analytical formula for the integral of the generalized sinc function
allows some formulas to be expressed simply (Knuth 1992; Knuth 1997, p. 57), and an example of which is the beautiful analytical formula for the integral of the generalized sinc function
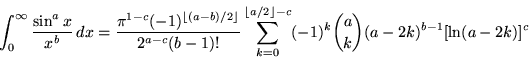
given by Kogan, where ![]() ,
,![]() ,
,![]() is the floor function.
is the floor function.
Richardson's theorem is a fundamental result in decidability theory which establishes that the determination of whether even simple expressions are identically equal to zero is undecidable in principle, let alone in practice.
The following table gives the first few numbers n such that the decimal expansion of ![]() contains no zeros for small k (a problem that resembles Gelfand's question.) The largest known n for which
contains no zeros for small k (a problem that resembles Gelfand's question.) The largest known n for which ![]() contain no zeros is 86 (Madachy 1979), with no other
contain no zeros is 86 (Madachy 1979), with no other ![]() (M. Cook), improving the
(M. Cook), improving the ![]() limit obtained by Beeler and Gosper (1972). The values a(n) such that the positions of the rightmost zero in
limit obtained by Beeler and Gosper (1972). The values a(n) such that the positions of the rightmost zero in ![]() increases are 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, ... (Sloane's A031140). The positions in which the rightmost zeros occur are 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, ... (Sloane's A031141). The rightmost zero of
increases are 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, ... (Sloane's A031140). The positions in which the rightmost zeros occur are 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, ... (Sloane's A031141). The rightmost zero of ![]() occurs at the 217th decimal place, the farthest over for powers up to
occurs at the 217th decimal place, the farthest over for powers up to ![]() .
.
| k | Sloane | n such that |
| 2 | A007377 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, ... |
| 3 | A030700 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, ... |
| 4 | A030701 | 1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, ... |
| 5 | A008839 | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, ... |
| 6 | A030702 | 1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, ... |
| 7 | A030703 | 1, 2, 3, 6, 7, 10, 11, 19, 35 |
| 8 | A030704 | 1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27 |
| 9 | A030705 | 1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34 |
| 11 | A030706 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, ... |
While it has not been proven that the numbers listed above are the only ones without zeros for a given base, the probability that any additional ones exist is vanishingly small. Under this assumption, the sequence of largest n such that ![]() contains no zeros for k = 2, 3, ... is then given by 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, ... (Sloane's A020665).
contains no zeros for k = 2, 3, ... is then given by 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, ... (Sloane's A020665).
![]()
10, Approximate Zero, Constant Problem, Division by Zero, Fallacy, Identically Zero, Naught, Negative, Nonnegative, Nonzero, One, Positive, Richardson's Theorem, Two, Uniformity Conjecture, Vanishing, Vanish Identically, Zerofree
![]()
![]()
Beeler, M. and Gosper, R. W. Item 57 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 22, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/number.html#item57.
Knuth, D. E. "Two Notes on Notation." Amer. Math. Monthly 99, 403-422, 1992.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 57, 1997.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 127-128, 1979.
Pappas, T. "Zero-Where & When." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 162, 1989.
Sloane, N. J. A. Sequences A007377/M0485 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 23-26, 1986.