The Farey sequence 
for any positive integer n is the set of irreducible rational numbers 
with 
and 
arranged in increasing order. The first few are
 |
 |
 |
(1) |
 |
|
 |
(2) |
 |
|
 |
(3) |
 |
|
 |
(4) |
 |
|
 |
(5) |
(Sloane's A006842 and A006843). Except for
, has an odd number of terms and the middle term is always 1/2.
Let 
,
,
be three successive terms in a Farey series. Then
 |
(6) |
 |
(7) |
These two statements are actually equivalent (Hardy and Wright 1979, p. 24). For a method of computing a successive sequence from an existing one of n terms, insert the mediant fraction 
between terms 
and 
when 
(Hardy and Wright 1979, pp. 25-26; Conway and Guy 1996; Apostol 1997). Given 
with 
,
be the mediant of and 
.
,
 |
(8) |
 |
(9) |
(Apostol 1997, p. 99).
The number of terms N(n) in the Farey sequence for the integer n is
 |
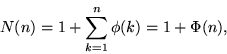(10) |
where 
is the totient function and 
is the summatory function of ,
 |
(11) |
(Vardi 1991, p. 155).
Ford circles provide a method of visualizing the Farey sequence. The Farey sequence defines a subtree of the Stern-Brocot tree obtained by pruning unwanted branches (Graham et al. 1994).
Ford Circle, Mediant, Minkowski's Question Mark Function, Sequence Rank, Stern-Brocot Tree
Apostol, T. M. "Farey Fractions." §5.4 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 97-99, 1997.
Beiler, A. H. "Farey Tails." Ch. 16 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Bogomolny, A. "Farey Series, A Story." http://www.cut-the-knot.org/blue/FareyHistory.shtml.
Conway, J. H. and Guy, R. K. "Farey Fractions and Ford Circles." The Book of Numbers. New York: Springer-Verlag, pp. 152-154 and 156, 1996.
Devaney, R. "The Mandelbrot Set and the Farey Tree, and the Fibonacci Sequence." Amer. Math. Monthly 106, 289-302, 1999.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, pp. 155-158, 1952.
Farey, J. "On a Curious Property of Vulgar Fractions." London, Edinburgh and Dublin Phil. Mag. 47, 385, 1816.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 118-119, 1994.
Guy, R. K. "Mahler's Generalization of Farey Series." §F27 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 263-265, 1994.
Hardy, G. H. and Wright, E. M. "Farey Series and a Theorem of Minkowski." Ch. 3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 23-37, 1979.
Sloane, N. J. A. Sequences A005728/M0661, A006842/M0041, and A006843/M0081 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Sylvester, J. J. "On the Number of Fractions Contained in Any Farey Series of Which the Limiting Number is Given." London, Edinburgh and Dublin Phil. Mag. (5th Series) 15, 251, 1883.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 155, 1991.