The Bernoulli numbers ![]() are a sequence of signed rational numbers that can be defined by the identity
are a sequence of signed rational numbers that can be defined by the identity
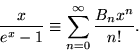 |
(1) |
These numbers arise in the series expansions of trigonometric functions, and are extremely important in number theory and analysis.
There are actually two definitions for the Bernoulli numbers. To distinguish them, the Bernoulli numbers as defined in modern usage (National Bureau of Standards convention) are written ![]() ,
,![]() (Gradshteyn and Ryzhik 2000). In each case, the Bernoulli numbers are a special case of the Bernoulli polynomials
(Gradshteyn and Ryzhik 2000). In each case, the Bernoulli numbers are a special case of the Bernoulli polynomials ![]() or
or ![]() with
with ![]() and
and ![]() .
.
Bernoulli numbers defined by the modern definition are denoted ![]() and sometimes called "even-index" Bernoulli numbers. These are the Bernoulli numbers returned, by example, by the Mathematica function BernoulliB[n].
and sometimes called "even-index" Bernoulli numbers. These are the Bernoulli numbers returned, by example, by the Mathematica function BernoulliB[n].
The Bernoulli number ![]() can be defined by the contour integral
can be defined by the contour integral
| (2) |
where the contour encloses the origin, has radius less than ![]() (to avoid the poles at
(to avoid the poles at ![]() ), and is traversed in a counterclockwise direction (Arfken 1985, p. 413).
), and is traversed in a counterclockwise direction (Arfken 1985, p. 413).
The first few Bernoulli numbers ![]() are
are
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
| (11) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (15) |
(Sloane's A000367 and A002445), with
| (16) |
for n = 1, 2, ....
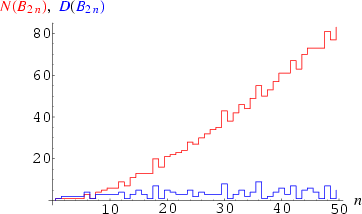
The numbers of digits in the numerator of ![]() for the n = 2, 4, ... are 1, 1, 1, 1, 1, 3, 1, 4, 5, 6, 6, 9, 7, 11, ... (Sloane's A068399), while the numbers of digits in the corresponding denominators are 1, 2, 2, 2, 2, 4, 1, 3, 3, 3, 3, 4, 1, 3, 5, 3, ... (Sloane's A092904). Both are plotted above.
for the n = 2, 4, ... are 1, 1, 1, 1, 1, 3, 1, 4, 5, 6, 6, 9, 7, 11, ... (Sloane's A068399), while the numbers of digits in the corresponding denominators are 1, 2, 2, 2, 2, 4, 1, 3, 3, 3, 3, 4, 1, 3, 5, 3, ... (Sloane's A092904). Both are plotted above.
The running maxima of denominators are 1, 6, 30, 42, 66, 2730, 14322, 1919190, ... (Sloane's A100194), which occur for n = 2, 4, 6, 8, 12, 14, 32, 38, ... (Sloane's A100195).
The number of digits in the numerator to ![]() for n = 0, 1, ... are 1, 1, 83, 1779, 27691, ... (Sloane's A103233).
for n = 0, 1, ... are 1, 1, 83, 1779, 27691, ... (Sloane's A103233).
![]() for 1806, but for no other n (Kellner 2005).
for 1806, but for no other n (Kellner 2005).
The only known Bernoulli numbers ![]() having prime numerators occur for n = 10, 12, 14, 16, 18, 36, and 42 (Sloane's A092132), corresponding to 5, -691, 7, -3617, 43867, -26315271553053477373, and 1520097643918070802691 (Sloane's A092133), with no other primes for
having prime numerators occur for n = 10, 12, 14, 16, 18, 36, and 42 (Sloane's A092132), corresponding to 5, -691, 7, -3617, 43867, -26315271553053477373, and 1520097643918070802691 (Sloane's A092133), with no other primes for ![]() (E. W. Weisstein, Apr. 17, 2005).
(E. W. Weisstein, Apr. 17, 2005).
The following table summarizes record computations of the nth Bernoulli number ![]() .
.![]() ) are downloadable from http://www.bernoulli.org/. The program Calcbn for Windows and Linux can be used to calculate Bernoulli numbers up to index
) are downloadable from http://www.bernoulli.org/. The program Calcbn for Windows and Linux can be used to calculate Bernoulli numbers up to index ![]() extremely quickly (Kellner).
extremely quickly (Kellner).
| n | digits in numerator | date | reference |
| Fee and Plouffe | |||
| 2002 | Plouffe (2002) | ||
| Dec. 16, 2002 | Kellner | ||
| |
Feb. 10, 2003 | Kellner |
The denominator of ![]() (mod 1) is given by the von Staudt-Clausen theorem, which also implies that the denominator of
(mod 1) is given by the von Staudt-Clausen theorem, which also implies that the denominator of ![]() is squarefree (Hardy and Wright 1979). Another curious property is that the fraction part of
is squarefree (Hardy and Wright 1979). Another curious property is that the fraction part of ![]() in decimal has a decimal period which divides n, and there is a single digit before that period (Conway 1996).
in decimal has a decimal period which divides n, and there is a single digit before that period (Conway 1996).
Consider the generating function
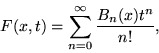 |
(17) |
which converges uniformly for ![]() and all x (Castellanos 1988). Taking the partial derivative gives
and all x (Castellanos 1988). Taking the partial derivative gives
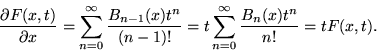 |
(18) |
The solution to this differential equation can be found using separation of variables as
| (19) |
so integrating gives
| (20) |
But integrating (20) explicitly gives
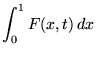 |
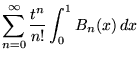 |
||
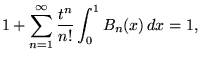 |
(21) |
so
| (22) |
Solving for T(t) and plugging back into (19) then gives
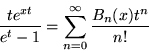 |
(23) |
(Castellanos 1988). Setting x = 0 and adding ![]() to both sides then gives
to both sides then gives
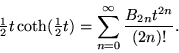 |
(24) |
Letting ![]() then gives
then gives
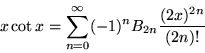 |
(25) |
for ![]() .
.
The Bernoulli numbers may also be calculated from
| (26) |
The Bernoulli numbers are given by the double sum
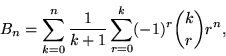 |
(27) |
where ![]() is a binomial coefficient. They also satisfy the sum
is a binomial coefficient. They also satisfy the sum
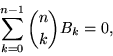 |
(28) |
as well as the interesting sums
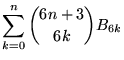 |
(29) | ||
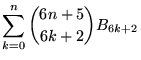 |
(30) |
(Lehmer 1935, Carlitz 1968), as well as the nice sum identity
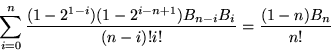 |
(31) |
(Gosper).
An asymptotic expansion for the even Bernoulli numbers is
| (32) |
Bernoulli numbers appear in expressions of the form ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
An analytic solution exists for even orders,
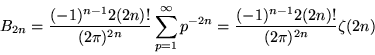 |
(33) |
for n = 1, 2, ..., where ![]() is the Riemann zeta function. Another intimate connection with the Riemann zeta function is provided by the identity
is the Riemann zeta function. Another intimate connection with the Riemann zeta function is provided by the identity
| (34) |
An integral in terms of the Euler polynomial is given by
| (35) |
where ![]() is an Euler polynomial (J. Crepps, pers. comm., Apr. 2002).
is an Euler polynomial (J. Crepps, pers. comm., Apr. 2002).
Bernoulli first used the Bernoulli numbers while computing ![]() .
.
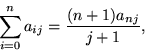 |
(36) |
along with a form for ![]() which he derived inductively to compute the sums up to n = 10 (Boyer 1968, p. 85). For
which he derived inductively to compute the sums up to n = 10 (Boyer 1968, p. 85). For ![]() ,
,
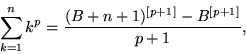 |
(37) |
where the notation ![]() means the quantity in question is raised to the appropriate power k, and all terms of the form
means the quantity in question is raised to the appropriate power k, and all terms of the form ![]() are replaced with the corresponding Bernoulli numbers
are replaced with the corresponding Bernoulli numbers ![]() .
.![]() with the understanding that after expansion,
with the understanding that after expansion, ![]() is replaced by
is replaced by ![]() .
.
Written explicitly in terms of a sum of powers,
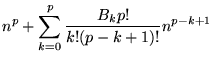 |
(38) | ||
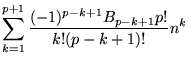 |
(39) | ||
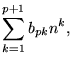 |
(40) |
where
| (41) |
It is also true that the coefficients of the terms ![]() sum to 1,
sum to 1,
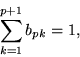 |
(42) |
which Bernoulli stated without proof.
Ramanujan ![]() gave a number of curious infinite sum identities involving Bernoulli numbers (Berndt 1994).
gave a number of curious infinite sum identities involving Bernoulli numbers (Berndt 1994).
The older definition of the Bernoulli numbers, no longer in widespread use, defines ![]() using the equations
using the equations
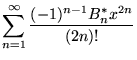 |
|||
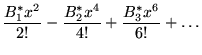 |
(43) |
for
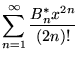 |
|||
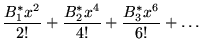 |
(44) |
for
| (45) |
and analytically from
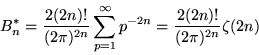 |
(46) |
for n = 1, 2, ..., where ![]() is the Riemann zeta function.
is the Riemann zeta function.
The Bernoulli numbers ![]() are a superset of the archaic ones
are a superset of the archaic ones ![]() since
since
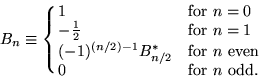 |
(47) |
The first few Bernoulli numbers ![]() are
are
| (48) | |||
| (49) | |||
| (50) | |||
| (51) | |||
| (52) | |||
| (53) | |||
| (54) | |||
| (55) | |||
| (56) | |||
| (57) | |||
| (58) |
![]()
Agoh's Conjecture, Bernoulli Function, Bernoulli Number of the Second Kind, Bernoulli Polynomial, Debye Functions, Euler-Maclaurin Integration Formulas, Euler Number, Figurate Number Triangle, Genocchi Number, Integer Sequence Primes, Irregular Prime, Modified Bernoulli Number, Pascal's Triangle, Riemann Zeta Function, von Staudt-Clausen Theorem
![]()
![]()
Abramowitz, M. and Stegun, I. A. (Eds.). "Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula." §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Arfken, G. "Bernoulli Numbers, Euler-Maclaurin Formula." §5.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 327-338, 1985.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 71, 1987.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 81-85, 1994.
Boyer, C. B. "Pascal's Formula for the Sums of Powers of the Integers." Scripta Math. 9, 237-244, 1943.
Boyer, C. B. A History of Mathematics. New York: Wiley, 1968.
Carlitz, L. "Bernoulli Numbers." Fib. Quart. 6, 71-85, 1968.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 107-110, 1996.
Dilcher, K. and Slavutskii, I. Sh. "A Bibliography of Bernoulli Numbers." http://www.mathstat.dal.ca/~dilcher/bernoulli.html.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Bernoulli Numbers." §6.5 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 283-290, 1994.
Hardy, G. H. and Wright, W. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 91-93, 1979.
Hauss, M. Verallgemeinerte Stirling, Bernoulli und Euler Zahlen, deren Anwendungen und schnell konvergente Reihen für Zeta Funktionen. Aachen, Germany: Verlag Shaker, 1995.
Havil, J. "Bernoulli Numbers." §10.1 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 81-84, 2003.
Ireland, K. and Rosen, M. "Bernoulli Numbers." Ch. 15 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 228-248, 1990.
Kellner, B. C. "The Bernoulli Number Page." http://www.bernoulli.org/.
Kellner, B. C. "The Equation ![]() Has Only One Solution." Apr. 2, 2005. http://www.bernoulli.org/~bk/denombneqn.pdf.
Has Only One Solution." Apr. 2, 2005. http://www.bernoulli.org/~bk/denombneqn.pdf.
Knuth, D. E. and Buckholtz, T. J. "Computation of Tangent, Euler, and Bernoulli Numbers." Math. Comput. 21, 663-688, 1967.
Lehmer, D. H. "Lacunary Recurrences for the Bernoulli Numbers." Ann. Math. 36, 637-649, 1935.
Nielsen, N. Traité élémentaire des nombres de Bernoulli. Paris: Gauthier-Villars, 1923.
Oakes, M. "Re: Prime Bernoulli Numerators." primenumbers group. Feb. 11, 2004. http://groups.yahoo.com/group/primenumbers/message/14550.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Plouffe, S. "The ![]() th Bernoulli Number." May 21, 2002. http://www.lacim.uqam.ca/~plouffe/ber500000.txt.
th Bernoulli Number." May 21, 2002. http://www.lacim.uqam.ca/~plouffe/ber500000.txt.
Ramanujan, S. "Some Properties of Bernoulli's Numbers." J. Indian Math. Soc. 3, 219-234, 1911.
Roman, S. The Umbral Calculus. New York: Academic Press, p. 31, 1984.
Sloane, N. J. A. Sequences A000367/M4039, A002445/M4189, A068399, A092132, A092132, A092904, A100194, A100195, and A103233 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Spanier, J. and Oldham, K. B. "The Bernoulli Numbers, ![]() .
.
Tanner, J. W. and Wagstaff, S. S. Jr. "New Congruences for the Bernoulli Numbers." Math. Comput. 48, 341-350, 1987.
Wagstaff, S. S. Jr. "Ramanujan's Paper on Bernoulli Numbers." J. Indian Math. Soc. 45, 49-65, 1981.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Woon, S C. "Generalization of a Relation Between the Riemann Zeta Function and Bernoulli Numbers." 24 Dec 1998. http://arxiv.org/abs/math.NT/9812143/.
Young, P. T. "Congruences for Bernoulli, Euler, and Stirling Numbers." J. Number Th. 78, 204-227, 1999.
![]()