Een even getal is een integer in de vorm van , waarbij k integer is. Een even getal is daarom bv ..., -4, -2, 0, 2, 4, 6, 8, 10, ... (Sloane's A005843). Daar de even getallen volledig deelbaar zijn door 2 , is er de congruentie voor even n. Een even getal voor welke geld nomet men ook een singulier even getal, en waar geld dat voor het getal n nomet men dit getal een dubbel even getal. Een itgere welke niet even is noemt men een oneven getal.

De onevenheid van een getal noemt men de pariteit, zo heeft een oneven getal een parity van 1,en een even getal een pariteit 0.

Een even getal is een natuurlijk of geheel getal dat als je het door 2 deelt, weer een natuurlijk getal oplevert zonder dat er een rest van de deling overblijft. Een evenredige definitie is een natuurlijk getal dat een veelvoud is van 2 (of: een even getal is deelbaar door 2). Een natuurlijk of geheel getal dat niet even is, heet oneven.

Je kunt bijvoorbeeld even getallen vormen, door twee gelijke natuurlijke getallen bij elkaar op te tellen:

Stelling: de som van twee gelijke, natuurlijke getallen is altijd een even getal

Bewijs: Zij

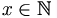
• Stel, x is even. Dan geldt dus 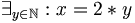. Maar dan geldt dus x + x = 2 * 2 * y, wat duidelijk weer een even getal is.
• Stel, x is niet even. Dan geldt dus 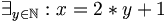. Maar dan x + x = 2 * (2 * y + 1) = 2 * 2 * y + 2, ook weer duidelijk een even getal.

Op soortgelijke wijze kan ook weer bewezen worden dat de som van twee even getallen altijd weer een even getal is en ook dat de som van twee oneven getallen een even getal is. Voor de som van een even en oneven getal geldt dit niet: 3 + 6 is immers 9.

De verzameling der even getallen kan op verschillende manieren worden weergegeven, zoals:

• 
• 
• 
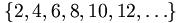
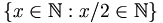
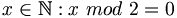
• {x:x is even}
• 
• 

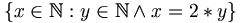
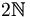
De verzameling van de even getallen is gesloten onder optellen en vermenigvuldigen: elke optelling van twee even getallen levert een even getal, en elke vermenigvuldiging van twee even getallen levert een even getal.

De verzameling van de even getallen bezit géén neutraal element voor de vermenigvuldiging (weliswaar is 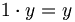voor elk even getal y, echter 1 behoort niet tot de verzameling van de even getallen).

Verder is de cardinaliteit van de verzameling even getallen gelijk aan die van de natuurlijke getallen, namelijk 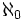, oftewel er zijn evenveel even getallen als er natuurlijke getallen zijn (voor geïnteresseerden, x = 2 * y is een mogelijk isomorfisme). Toch is de verzameling even getallen een echte deelverzameling van die van de natuurlijke getallen. Dit is mogelijk, doordat beide verzamelingen oneindig zijn, precieser: aftelbaar oneindig.

The generating function of the even numbers is

The product of an even number and an odd number is always even, as can be seen by writing

which is divisible by 2 and hence is even.

.

Doubly Even Number, Even Function, Odd Number, Parity, Singly Even Number