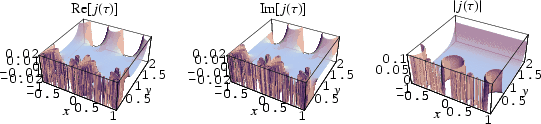
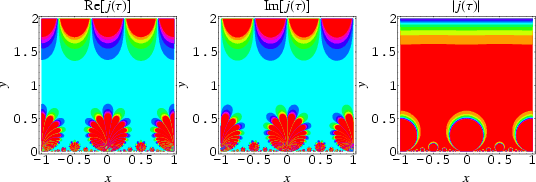
The j-function is the modular function defined by
| (1) |
where ![]() is the half-period ratio,
is the half-period ratio, ![]() ,
,
| (2) |
is Klein's absolute invariant, ![]() is the elliptic lambda function
is the elliptic lambda function
| (3) |
| (4) |
is the nome, and ![]() .
.
Gauss was apparently aware of the j-function before 1800. Hermite used it in solving the quintic in about 1858. Dedekind gave a nice definition in about 1877, and Klein studied the function beginning in 1879 or 1880. The j-function is related to the factors of the group order of the monster group and to supersingular primes (Ogg 1980).
This function can also be specified in terms of the Weber functions f, ![]() ,
,![]() ,
,![]() ,
,![]() as
as
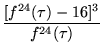 |
(5) | ||
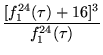 |
(6) | ||
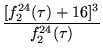 |
(7) | ||
| (8) | |||
| (9) |
(Weber 1902, p. 179; Atkin and Morain 1993).
The j-function is an analytic function on the upper half-plane which is invariant with respect to the special linear group ![]() .
.
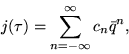 |
(10) |
where
| (11) |
The coefficients in the expansion of the j-function satisfy:
- 1.
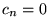 for n < -1 and
for n < -1 and 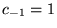 ,
, - 2. all
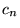 s are integers with fairly limited growth with respect to n, and
s are integers with fairly limited growth with respect to n, and - 3.
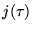 is an algebraic number, sometimes a rational number, and sometimes even an integer at certain very special values of
is an algebraic number, sometimes a rational number, and sometimes even an integer at certain very special values of 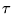 .
.
Therefore all of the coefficients in the Laurent series
| |
|
| |
(12) |
Some remarkable sum formulas involving ![]() for
for ![]() ,
,
| (13) |
and
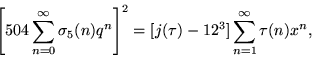 |
(14) |
where ![]() is the divisor function and
is the divisor function and ![]() .
.
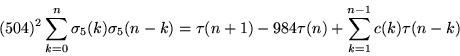 |
(15) |
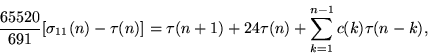 |
(16) |
where ![]() is the tau function (Lehmer 1942; Apostol 1997, p. 92), not to be confused with the half-period ratio
is the tau function (Lehmer 1942; Apostol 1997, p. 92), not to be confused with the half-period ratio ![]() .
.
Equation (16) leads immediately to the remarkable congruence
| (17) |
Lehmer (1942) showed that
| (18) |
for all ![]() ,
,
| |
(19) |
| |
(20) |
| |
(21) |
| |
(22) |
| |
(23) |
| |
(24) |
| |
(25) |
| |
(26) |
| |
(27) |
| (28) |
where ![]() and
and ![]() if x is not an integer (Apostol 1997, p. 91). Congruences for
if x is not an integer (Apostol 1997, p. 91). Congruences for ![]() have been generalized by Atkin and O'Brien (1967).
have been generalized by Atkin and O'Brien (1967).
An asymptotic formula for c(n) was discovered by Petersson (1932), and subsequently independently rediscovered by Rademacher (1938):
| (29) |
Let d be a squarefree positive integer, and define the half-period ratio by
| (30) |
so
| (31) |
It then turns out that ![]() is an algebraic integer of degree
is an algebraic integer of degree ![]() ,
,![]() is the class number of the binary quadratic form discriminant
is the class number of the binary quadratic form discriminant ![]() of the quadratic field
of the quadratic field ![]() (Silverman 1986; Berndt 1994, p. 90).
(Silverman 1986; Berndt 1994, p. 90).
If ![]() ,
,![]() is a algebraic integer of degree 1, i.e., just a plain integer. Furthermore, the integer is a perfect cube. But these are precisely the Heegner numbers -1, -2, -3, -7, -11, -19, -43, -67, -163. The exact values of
is a algebraic integer of degree 1, i.e., just a plain integer. Furthermore, the integer is a perfect cube. But these are precisely the Heegner numbers -1, -2, -3, -7, -11, -19, -43, -67, -163. The exact values of ![]() corresponding to the Heegner numbers are
corresponding to the Heegner numbers are
| (32) | |||
| (33) | |||
| (34) | |||
| (35) | |||
| (36) | |||
| (37) | |||
| (38) | |||
| (39) | |||
| (40) |
The positions of these special values of
The greater (in absolute value) the Heegner number d, the closer to an integer is the expression ![]() ,
,![]() is the largest and subsequent terms are the smallest. The best approximations with
is the largest and subsequent terms are the smallest. The best approximations with ![]() are therefore
are therefore
| (41) | |||
| (42) | |||
| (43) |
(the latter of which appears in Trott 2004, p. 8). The almost integer generated by the last of these,
There are 18 numbers having class number ![]() ,
,
| (44) | |||
| (45) | |||
| (46) | |||
| (47) |
and so on.
The numbers
| (48) | |||
| (49) | |||
| (50) |
are also almost integers. These correspond to binary quadratic forms with discriminants -88, -148, and -232, which are the largest (in absolute value) discriminants with class number two that are divisible by 4. They were noted by Ramanujan
![]()
Almost Integer, Heegner Number, Imaginary Quadratic Field, Klein's Absolute Invariant, Monster Group, Ramanujan Constant, Supersingular Prime, Weber Functions
![]()
![]()
Apostol, T. M. "The Fourier Expansions of ![]() and
and ![]() " and "Congruences for the Coefficients of the Modular Function j." §1.15 and Ch. 4 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 20-22 and 74-93, 1997.
" and "Congruences for the Coefficients of the Modular Function j." §1.15 and Ch. 4 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 20-22 and 74-93, 1997.
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Atkin, A. O. L. and O'Brien, J. N. "Some Properties of p(n) and c(n) Modulo Powers of 13." Trans. Amer. Math. Soc. 126, 442-459, 1967.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Berwick, W. E. H. "An Invariant Modular Equation of the Fifth Order." Quart. J. Math. 47, 94-103, 1916.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 117-118, 1987.
Cohen, H. In From Number Theory to Physics (M. Waldschmidt, P. Moussa, J.-M. Luck, and C. Itzykson). Berlin: Springer-Verlag, 1992.
Cohn, H. Introduction to the Construction of Class Fields. New York: Dover, p. 73, 1994.
Conway, J. H. and Guy, R. K. "The Nine Magic Discriminants." In The Book of Numbers. New York: Springer-Verlag, pp. 224-226, 1996.
Hermite, C. "Sur la théorie des équations modulaires." Comptes Rendus Acad. Sci. Paris 49, 16-24, 110-118, and 141-144, 1859 Oeuvres complètes, Tome II. Paris: Hermann, p. 61, 1912.
Lehmer, D. H. "Properties of the Coefficients of the Modular Invariant ![]() .
.
Lehner, J. "Divisibility Properties of the Fourier Coefficients of the Modular Invariant ![]() .
.
Lehner, J. "Further Congruence Properties of the Fourier Coefficients of the Modular Invariant ![]() .
.
Morain, F. "Implementation of the Atkin-Goldwasser-Kilian Primality Testing Algorithm." Rapport de Recherche 911, INRIA, Oct. 1988.
Newman, M. "Congruences for the Coefficients of Modular Forms and for the Coefficients of ![]() .
.
Ogg, A. P. "Modular Functions." In The Santa Cruz Conference on Finite Groups. Held at the University of California, Santa Cruz, Calif., June 25-July 20, 1979 (Ed. B. Cooperstein and G. Mason). Providence, RI: Amer. Math. Soc., pp. 521-532, 1980.
Petersson, H. "Über die Entwicklungskoeffizienten der automorphen formen." Acta Math. 58, 169-215, 1932.
Rademacher, H. "The Fourier Coefficients of the Modular Invariant ![]() .
.
Rankin, R. A. Modular Forms. New York: Wiley, 1985.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, p. 199, 1977.
Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., 1992.
Serre, J.-P. A Course in Arithmetic. New York: Springer-Verlag, 1973.
Silverman, J. H. The Arithmetic of Elliptic Curves. New York: Springer-Verlag, p. 339, 1986.
Sloane, N. J. A. Sequences A000521/M5477 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Stillwell, J. "Modular Miracles." Amer. Math. Monthly 108, 70-76, 2001.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
van Wijngaarden, A. "On the Coefficients of the Modular Invariant ![]() .
.
Waldschmidt, M. In Ramanujan Centennial International Conference (Ed. R. Balakrishnan, K. S. Padmanabhan, and V. Thangaraj). Ramanujan Math. Soc., 1988.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1979.
Zuckerman, H. S. "The Computation of the Smaller Coefficients of ![]() .
.
![]()