Just as the ratio of a the arc length of a semicircle to its radius is always ![]() ,
,
| (1) | |||
| (2) | |||
| (3) | |||
| (4) |
(Sloane's A103710). This can be seen from the equation of the arc length of a parabolic segment
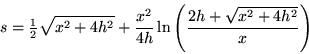 |
(5) |
by taking ![]() and plugging in h = a and
and plugging in h = a and ![]() .
.
The other conic sections, namely the ellipse and hyperbola, do not have such universal constants because the analogous ratios for them depend on their eccentricities. In other words, all circles are similar and all parabolas are similar, but the same is not true for ellipses or hyperbolas (Ogilvy 1969, p. 84).
The area of the surface generated by revolving ![]() for
for ![]() about the y-axis is given by
about the y-axis is given by
| (6) | |||
| (7) |
(Love 1950, p. 288; Sloane's A103713) and the area of the surface generated by revolving
| (8) | |||
| (9) |
(Love 1950, p. 288; Sloane's A103714).
The expected distance from a randomly selected point in the unit square to its center (square point picking) is
| (10) | |||
| (11) |
(Finch 2003, p. 479; Sloane's A103712).
P is an irrational number. It is also a transcendental number, as can be seen as follows. If P were algebraic, then ![]() would also be algebraic. But then, by the Lindemann-Weierstrass theorem,
would also be algebraic. But then, by the Lindemann-Weierstrass theorem, ![]() would be transcendental, which is a contradiction.
would be transcendental, which is a contradiction.
![]()
Focal Parameter, Latus Rectum, Lindemann-Weierstrass Theorem, Parabola, Parabolic Segment, Semilatus Rectum
![]()
![]()
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Love, C. E. Differential and Integral Calculus, 4th ed. New York: Macmillan, 1950.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, 1990.
Sloane, N. J. A. Sequences A103710, A103711, A103712, A103713, and A103714 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.