If there is an integer ![]() such that
such that
| (1) |
then q is said to be a quadratic residue (mod p). If not, q is said to be a quadratic nonresidue (mod p). Hardy and Wright (1979, pp. 67-68) use the shorthand notations ![]() and
and ![]() ,
,
For example, ![]() ,
,
| |
(2) |
| |
(3) |
| |
(4) |
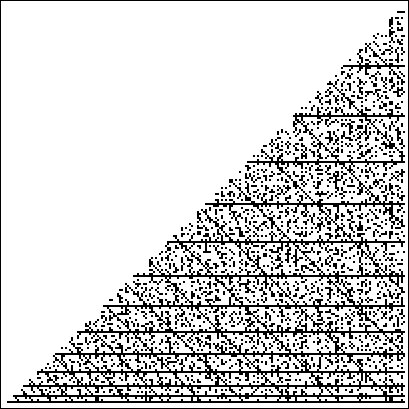
A list of quadratic residues for ![]() is given below (Sloane's A046071), with those numbers
is given below (Sloane's A046071), with those numbers ![]() not in the list being quadratic nonresidues of p.
not in the list being quadratic nonresidues of p.
| p | quadratic residues |
| 1 | (none) |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1, 4 |
| 6 | 1, 3, 4 |
| 7 | 1, 2, 4 |
| 8 | 1, 4 |
| 9 | 1, 4, 7 |
| 10 | 1, 4, 5, 6, 9 |
| 11 | 1, 3, 4, 5, 9 |
| 12 | 1, 4, 9 |
| 13 | 1, 3, 4, 9, 10, 12 |
| 14 | 1, 2, 4, 7, 8, 9, 11 |
| 15 | 1, 4, 6, 9, 10 |
| 16 | 1, 4, 9 |
| 17 | 1, 2, 4, 8, 9, 13, 15, 16 |
| 18 | 1, 4, 7, 9, 10, 13, 16 |
| 19 | 1, 4, 5, 6, 7, 9, 11, 16, 17 |
| 20 | 1, 4, 5, 9, 16 |
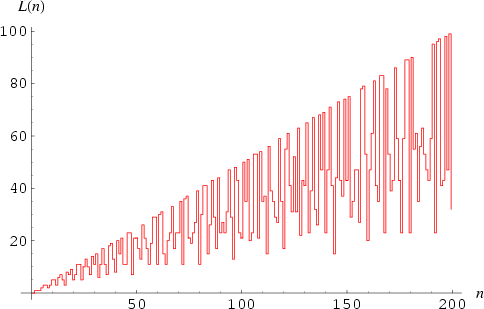
The numbers of quadratic residues (mod n) for n = 1, 2, ... are 0, 1, 1, 1, 2, 3, 3, 2, 3, 5, 5, 3, 6, 7, 5, 3, ... (Sloane's A105612).
![]()
The largest quadratic residues for p = 2, 3, ... are 1, 1, 1, 4, 4, 4, 4, 7, 9, 9, 9, 12, 11, ... (Sloane's A047210).
Given an odd prime p and an integer a, then the Legendre symbol is given by
| (5) |
If
| (6) |
then r is a quadratic residue (+) or nonresidue (![]() ). This can be seen since if r is a quadratic residue of p, then there exists a square
). This can be seen since if r is a quadratic residue of p, then there exists a square ![]() such that
such that ![]() ,
,
| (7) |
and ![]() is congruent to 1 (mod p) by Fermat's little theorem.
is congruent to 1 (mod p) by Fermat's little theorem.
Given p and q in the congruence
| (8) |
x can be explicitly computed for p and q of certain special forms:
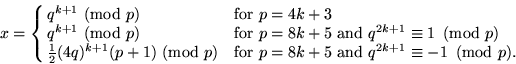 |
(9) |
For example, the first form can be used to find x given the quadratic residues q = 1, 3, 4, 5, and 9 (mod p = 11, having k = 2), whereas the second and third forms determine x given the quadratic residues q = 1, 3, 4, 9, 10, and 12 (mod p = 13, having k = 1), and q = 1, 3, 4, 7, 9, 10, 11, 12, 16, 21, 25, 26, 27, 28, 30, 33, 34, 36 (mod p = 37, having k = 4).
More generally, let q be a quadratic residue modulo an odd prime p. Choose h such that the Legendre symbol ![]() .
.
| (10) | |||
| (11) | |||
| (12) |
gives
| (13) | |||
| (14) |
and a solution to the quadratic congruence is
| (15) |
Schoof (1985) gives an algorithm for finding x with running time ![]() (Hardy et al. 1990). The congruence is solved by the Mathematica command SqrtMod[q, p] in the Mathematica add-on package NumberTheory`NumberTheoryFunctions` (which can be loaded with the command <<NumberTheory`).
(Hardy et al. 1990). The congruence is solved by the Mathematica command SqrtMod[q, p] in the Mathematica add-on package NumberTheory`NumberTheoryFunctions` (which can be loaded with the command <<NumberTheory`).
The following table gives the primes which have a given number d as a quadratic residue.
| d | Primes |
| -6 | |
| -5 | |
| -3 | |
| -2 | |
| -1 | |
| 2 | |
| 3 | |
| 5 | |
| 6 |
Finding the continued fraction of a square root ![]() and using the relationship
and using the relationship
| (16) |
for the nth convergent ![]() gives
gives
| (17) |
Therefore, ![]() is a quadratic residue of D. But since
is a quadratic residue of D. But since ![]() ,
,![]() is a quadratic residue, as must be
is a quadratic residue, as must be ![]() .
.![]() is a quadratic residue, so is
is a quadratic residue, so is ![]() ,
,![]() are all quadratic residues of D. This method is not guaranteed to produce all quadratic residues, but can often produce several small ones in the case of large D, enabling D to be factored.
are all quadratic residues of D. This method is not guaranteed to produce all quadratic residues, but can often produce several small ones in the case of large D, enabling D to be factored.
The number of squares s(n) in ![]() is related to the number q(n) of quadratic residues in
is related to the number q(n) of quadratic residues in ![]() by
by
| (18) |
for ![]() (Stangl 1996). Both q and s are multiplicative functions.
(Stangl 1996). Both q and s are multiplicative functions.
![]()
Associate, Euler's Criterion, Jacobi Symbol, Kronecker Symbol, Legendre Symbol, Multiplicative Function, Quadratic, Quadratic Nonresidue, Quadratic Reciprocity Theorem, Riemann Hypothesis
![]()
![]()
Burgess, D. A. "The Distribution of Quadratic Residues and Non-Residues." Mathematika 4, 106-112, 1975.
Burton, D. M. Elementary Number Theory, 4th ed. New York: McGraw-Hill, p. 201, 1997.
Courant, R. and Robbins, H. "Quadratic Residues." §2.3 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 38-40, 1996.
Guy, R. K. "Quadratic Residues. Schur's Conjecture" and "Patterns of Quadratic Residues." §F5 and F6 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 244-248, 1994.
Hardy, G. H. and Wright, E. M. "Quadratic Residues." §6.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 67-68, 1979.
Hilton, P.; Holton, D.; and Pedersen, J. Mathematical Reflections in a Room with Many Mirrors. New York: Springer-Verlag, p. 43, 1997.
Jones, G. A. and Jones, J. M. "Quadratic Residues." Ch. 7 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 119-141, 1998.
Nagell, T. "Theory of Quadratic Residues." Ch. 4 in Introduction to Number Theory. New York: Wiley, pp. 115 and 132-155, 1951.
Niven, I. and Zuckerman, H. An Introduction to the Theory of Numbers, 4th ed. New York: Wiley, p. 84, 1980.
Rosen, K. H. Ch. 9 in Elementary Number Theory and Its Applications, 3rd ed. Reading, MA: Addison-Wesley, 1993.
Schoof, R. "Elliptic Curves Over Finite Fields and the Computation of Square Roots mod p." Math. Comput. 44, 483-494, 1985.
Séroul, R. "Quadratic Residues." §2.10 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 17-18, 2000.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 63-66, 1993.
Sloane, N. J. A. Sequences A046071 and A047210 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Stangl, W. D. "Counting Squares in ![]() .
.
Tonelli, A. "Bemerkung über die Auflösung quadratischer Congruenzen." Göttingen Nachr., 344-346, 1891.
Wagon, S. "Quadratic Residues." §9.2 in Mathematica in Action. New York: W. H. Freeman, pp. 292-296, 1991.
Wedeniwski, S. "Primality Tests on Commutator Curves." Dissertation. Tübingen, Germany, 2001. http://www.hipilib.de/prime/primality-tests-on-commutator-curves.pdf.
![]()