A prime p for which ![]() has a maximal period decimal expansion of
has a maximal period decimal expansion of ![]() digits. Full reptend primes are sometimes also called long primes (Conway and Guy 1996, pp. 157-163 and 166-171).
digits. Full reptend primes are sometimes also called long primes (Conway and Guy 1996, pp. 157-163 and 166-171).
A prime p is full reptend iff 10 is a primitive root modulo p, which means that
| (1) |
for ![]() and no k less than this. In other words, the modulo order of p (mod 10) is
and no k less than this. In other words, the modulo order of p (mod 10) is ![]() .
.
For example, 7 is a full reptend prime since ![]() .
.
The full reptend primes are 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, ... (Sloane's A001913). The first few decimal expansions of these are
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |
Here, the numbers 142857, 5882352941176470, 526315789473684210, ... (Sloane's A004042) corresponding to the periodic parts of these decimal expansions are called cyclic numbers. No general method is known for finding full reptend primes.
The number of full reptend primes less than ![]() for n = 1, 2, ... are 1, 9, 60, 467, 3617, ... (Sloane's A086018).
for n = 1, 2, ... are 1, 9, 60, 467, 3617, ... (Sloane's A086018).
A necessary (but not sufficient) condition that p be a full reptend prime is that the number ![]() (where
(where ![]() is a repunit) is divisible by p, which is equivalent to
is a repunit) is divisible by p, which is equivalent to ![]() being divisible by p. For example, values of n such that
being divisible by p. For example, values of n such that ![]() is divisible by n are given by 1, 3, 7, 9, 11, 13, 17, 19, 23, 29, 31, 33, 37, ... (Sloane's A104381).
is divisible by n are given by 1, 3, 7, 9, 11, 13, 17, 19, 23, 29, 31, 33, 37, ... (Sloane's A104381).
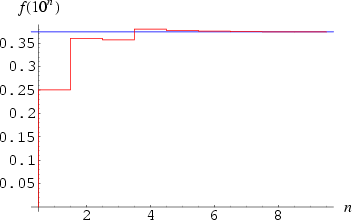
Artin conjectured that Artin's constant ![]() (Sloane's A005596) is the fraction of primes p for which
(Sloane's A005596) is the fraction of primes p for which ![]() has decimal maximal period (Conway and Guy 1996). The first few fractions include primes up to
has decimal maximal period (Conway and Guy 1996). The first few fractions include primes up to ![]() for n = 1, 2, ... are 1/4, 9/25, 5/14, 467/1229, 3617/9592, 14750/39249, ... (Sloane's A103362 and A103363), illustrated above, with the values of C illustrated in red. D. Lehmer has generalized this conjecture to other bases, obtaining values that are small rational multiples of C.
for n = 1, 2, ... are 1/4, 9/25, 5/14, 467/1229, 3617/9592, 14750/39249, ... (Sloane's A103362 and A103363), illustrated above, with the values of C illustrated in red. D. Lehmer has generalized this conjecture to other bases, obtaining values that are small rational multiples of C.
![]()
Artin's Constant, Cyclic Number, Decimal Expansion, Modulo Order, Primitive Root, Repeating Decimal, Unique Prime
![]()
![]()
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, 1996.
Sloane, N. J. A. Sequences A001913/M4353, A004042, A005596, A006883/M1745, A086018, A103362, A103363, and A104381 in "The On-Line Encyclopedia of Integer Sequences." http://www.research.att.com/~njas/sequences/.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 71, 1986.
![]()