The base 2 method of counting in which only the digits 0 and 1 are used. In this base, the number 1011 equals . This base is used in computers, since all numbers can be simply represented as a string of electrically pulsed ons and offs. In computer parlance, one binary digit is called a bit, two digits are called a crumb, four digits are called a nibble, and eight digits are called a byte.

An integer n may be represented in binary in Mathematica using the command BaseForm[n, 2], and the first d digits of a real number x may be obtained in binary using RealDigits[x, 2, d]. Finally, a list of binary digits l can be converted to a decimal rational number or integer using FromDigits[l, 2].

The illustration above shows the binary numbers from 0 to 63 represented graphically (Wolfram 2002, p. 117), and the following table gives the binary equivalents of the first few decimal numbers.

A negative number is most commonly represented in binary using the complement of the positive number , so would be written as the complement of , or 11110101. This allows addition to be carried out with the usual carrying and the leftmost digit discarded, so 17-11 = 6 gives

The number of times k that a given binary number is divisible by 2 is given by the position of the first counting from the right. For example, 12 = 1100 is divisible by 2 twice, and 13 = 1101 is divisible by 2 zero times. The number of times that 1, 2, ... are divisible by 2 are 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, 4, 0, 1, 0, 2, ... (Sloane's A007814), which is the binary carry sequence.

Real numbers can also be represented using binary notation by interpreting digits past the "decimal" point as negative powers of two, so the binary digits would represent the number

Therefore, 1/2 would be represented as , 1/4 as , 3/4 as , and so on. The sequence of binary digits for the integers n = 0, 1, ... concatenated together and interpreted as a binary constant give the binary Champernowne constant (Sloane's A030190).

Unfortunately, the storage of binary numbers in computers is not entirely standardized. Because computers store information in 8-bit bytes (where a bit is a single binary digit), depending on the "word size" of the machine, numbers requiring more than 8 bits must be stored in multiple bytes. The usual FORTRAN77 integer size is 4 bytes long. However, a number represented as (byte1 byte2 byte3 byte4) in a VAX would be read and interpreted as (byte4 byte3 byte2 byte1) on a Sun. The situation is even worse for floating-point (real) numbers, which are represented in binary as a mantissa and characteristic, and worse still for long (8-byte) reals!

Binary multiplication of single bit numbers (0 or 1) is equivalent to the AND operation, as can be seen in the following multiplication table.

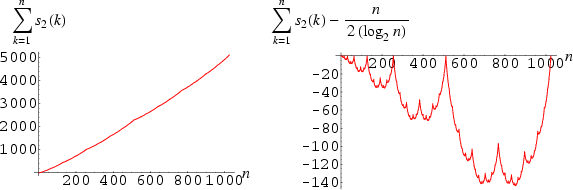
Consider the cumulative digit sum of all binary numbers up to 1, 2, ..., n. The first few terms are then 1, 2, 4, 5, 7, 9, 12, 13, 15, 17, 20, 22, ... (Sloane's A000788). This sequence in monotonic increasing (left figure), but if the main asymptotic term is removed, a sequence of humped curves (right figure; Trott 2004, p. 218) tending towards the Blancmange function is obtained.

 

Base, Binary Carry Sequence, Bit, Blancmange Function, Byte, Champernowne Constant, Crumb, Decimal, Digit Count, Eye of Horus Fraction, Factorial, Hexadecimal, Moser-de Bruijn Sequence, Negabinary, Nibble, Octal, Quaternary, Rudin-Shapiro Sequence, Stolarsky-Harborth Constant, Ternary